

Рис. 8.4.( а) Вид от любой монетки на бесконечном плоском листе такой же, как и вид от любой другой монетки. ( б) Чем дальше друг от друга расположены две монетки на ( а), тем быстрее будет увеличиваться расстояние между ними при растяжении плоскости
Одно замечательное обстоятельство, имеющее отношение как к сферическому пространству, так и к бесконечному плоскому пространству, заключается в том, что вы можете бесконечно идти по нему и никогда не достигнете края или границы. Это удобно, поскольку позволяет избежать каверзных вопросов: что находится за краем пространства? что произойдёт, если вы дойдёте до границы пространства? Если пространство не имеет краёв или границ, вопрос не имеет смысла. Но заметим, что эти две формы обеспечивают это привлекательное свойство пространства различными способами. Если вы идёте прямо вперёд в сферическом пространстве, вы обнаружите, подобно Магеллану, что рано или поздно вернётесь в стартовую точку, нигде не встретив край. Наоборот, если вы идёте прямо вперёд по бесконечному плоскому пространству, то обнаружите, что, подобно кролику Энерджайзеру, можете идти и идти и никогда не дойдёте до края, но и не вернётесь туда, откуда начали путешествие. Хотя это может показаться фундаментальным отличием между геометрией искривлённого и плоского пространства, имеется простая вариация плоского пространства, которое делает его поразительно похожим в этом отношении на сферу.
Чтобы проиллюстрировать это, вспомним одну из тех видеоигр, в которых кажется, что экран имеет края, но на самом деле их нет, поскольку реально вы не можете покинуть пределы экрана: если вы пытаетесь выйти за правый край, вы снова появляетесь на левом; если вы выходите за верхний край, то снова появляетесь на нижнем. Экран «зациклен» путём отождествления верхнего края с нижним, а левого с правым, и, таким образом, форма пространства плоская (неискривлённая), но имеет конечныйразмер и не имеет краёв. Математически эта форма называется двумерным тором, она проиллюстрирована на рис. 8.5 а. {111} Трёхмерный вариант этой формы — трёхмерный тор — обеспечивает другую возможную форму для ткани космоса. Вы можете представить себе эту форму как гигантский куб, который зациклен вдоль всех трёх направлений: когда вы проходите через потолок, вы снова появляетесь снизу, когда вы проходите через заднюю стенку куба, вы снова появляетесь из передней стенки, когда вы проходите через левую сторону, вы снова появляетесь из правой, как показано на рис. 8.5 б. Такая форма — плоская (в том смысле, что не искривлённая, а не в том смысле, что подобна блину), трёхмерная, конечная по всем направлениям и не имеет краёв и границ.

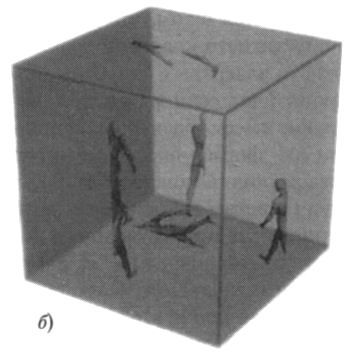
Рис. 8.5.( а) Экран видеоигры является плоским (в смысле «неискривлённым») и имеет конечный размер, но не содержит краёв или границ, поскольку он «зациклен». Математически такая форма называется двумерным тором. ( б) Трёхмерная версия той же формы, называемая трёхмерным тором, также плоская (в смысле «неискривлённая»), имеет конечный объём и тоже не имеет краёв или границ, поскольку зациклена. Если вы проходите через одну сторону куба, вы входите через противоположную сторону
Помимо этих возможностей, остаётся ещё и другая форма, согласующаяся с объяснением открытия Хаббла с помощью симметричного расширяющегося пространства. Хотя это трудно изобразить в трёх измерениях, но, как и в примере сферического пространства, имеется хорошая двумерная модель: бесконечный вариант картофельного чипса «Принглс». Эта форма, часто обозначаемая как седло, является некоей противоположностью сферы: в то время как сфера симметрично выпукла наружу, седловина симметрично вогнута в себя, как показано на рис. 8.6. Используя немного математической терминологии, скажем, что сфера имеет положительную кривизну(выпукла наружу), седловина имеет отрицательную кривизну(вогнута в себя), а плоское пространство — как бесконечное, так и конечное — не имееткривизны (не выпукло и не имеет седловидной формы). [57]


Рис. 8.6.Использование двумерных аналогий для полностью симметричных пространств, в которых вид из любой точки пространства такой же, как и из любой другой, с тремя различными типами кривизны. ( а) Положительнаякривизна, соответствующая однородной выпуклости, как у сферы. ( б) Нулеваякривизна, которая отвечает полному отсутствию выпуклости, как на бесконечной плоскости или конечном экране видеоигры. ( в) Отрицательнаякривизна, которая отвечает седловидной поверхности
Исследователи доказали, что этот список — однородно положительная, отрицательная или нулевая — исчерпывает возможные виды кривизны для пространства, которое соответствует требованию симметрии между всеми положениями и всеми направлениями. И это действительно потрясающе. Мы говорим о форме всей Вселенной— о чем-то, для чего имеется бесчисленное число возможностей. Однако, призвав великую силу симметрии, исследователи оказались в состоянии резко снизить число возможностей. Так что если вы позволите симметрии направлять ваш ответ, и ваш полуночный интервьюер даст вам несколько шансов для ответа, вы будете в состоянии принять его вызов. {112}
И всё же вы можете спросить: почему мы пришли к нескольким возможным формам для ткани пространства? Мы обитаем в одной Вселенной, так почему мы не можем точно указать на единственную форму? Только перечисленные формы гарантируют, что каждый наблюдатель, независимо от того, где во Вселенной он находится, должен видеть в больших масштабах одинаковый космос. Но такое применение симметрии, хотя и сильно ограничивает отбор, не даёт возможности полностью решить задачу и дать единственный ответ. Для этого нам нужны уравнения общей теории относительности Эйнштейна.
В качестве входных данных уравнения Эйнштейна принимают количество материи и энергии во Вселенной (предполагая, опять же из соображений симметрии, что они распределены равномерно), а на выходе они дают кривизну пространства. Сложность в том, что на протяжении многих десятилетий астрономы не могли прийти к согласию, сколько на самом деле имеется материи и энергии. Если вся материя и энергия во Вселенной была бы однородно распределена по пространству и если после этого оказалось бы, что превышена так называемая критическая плотность, которая составляет около 10 ?23г на каждый кубический метр [58] — около пяти атомов водорода на кубический метр, — уравнения Эйнштейна дали бы положительную кривизну пространства; если бы плотность оказалась меньше критической, уравнения привели бы к отрицательной кривизне; если плотность была бы в точности равна критической, уравнения показали бы, что пространство не имеет общей кривизны. В то время как эта наблюдательная проблема ещё ждёт определённого решения, наиболее точные данные склоняют стрелку в сторону отсутствия кривизны — плоской формы пространства (но вопрос о том, может ли кролик Энерджайзер всегда двигаться в одном направлении и исчезнуть в темноте или однажды он замкнёт круг и появится у вас за спиной — простирается ли пространство бесконечно или зациклено подобно видеоэкрану, — всё ещё полностью открыт). {113}
57
Точно так же, как экран видеоигры даёт версию плоского пространства конечного размера, которое не имеет краёв или границ, имеются версии пространства седловидной формы конечного размера, которые также не имеют краёв или границ. Я больше не буду обсуждать это, запомним лишь, что все три возможные кривизны (положительная, нулевая и отрицательная) могут быть реализованы в формах конечного размера без краёв или границ (и тогда космический Магеллан в принципе смог бы осуществить космическую версию своего путешествия во Вселенной, кривизна которой задана любой из трёх возможностей).
58
Сегодня материи во Вселенной больше, чем излучения, так что критическую плотность удобно выражать в единицах, наиболее подходящих для измерения массы, — граммы на кубический метр. Отметим также, что хотя плотность 10 ?23г на кубический метр может и не выглядит очень большой, в космосе очень многокубических метров пространства. Более того, оглядываясь назад во времени, вы увидите, что чем меньше пространство, по которому распределена материя/энергия, тем более плотной становится Вселенная.
