В этой главе вероятность также будет играть центральную роль. Но, поскольку вероятность являетсянеизбежным элементом квантовой механики, это фундаментально меняет наше представление о прошлом и будущем. Мы уже видели, что квантовая неопределённость не допускает одновременного знания точных положений и точных скоростей. Мы также видели, что квантовая физика предсказывает только вероятность реализации того или иного будущего. Мы уверены в этих вероятностях, но, поскольку это всё же вероятности, ясно, что имеется неизбежныйэлемент случайности при попытке предсказать будущее.
Когда приходится описывать прошлое, между классической и квантовой физикой также имеется важное отличие. В классической физике, в связи с её равноправным рассмотрением всех моментов времени, события, приводящие к чему-нибудь, что мы наблюдаем, описываются с использованием в точности того же языка, с применением в точности тех же характерных свойств, которые мы используем для описания самого наблюдения. Если мы видим огненный метеор в ночном небе, мы говорим о его положении и скорости; если мы воссоздаём картину его появления там, мы также говорим об однозначной последовательности положений и скоростей, когда метеор нёсся через пространство к Земле. В квантовой физике, когда мы что-то наблюдаем, мы входим в особое царство, где что-то может быть известно со 100%-й определённостью (игнорируя проблемы, связанные с точностью приборов, и подобные им). Но прошлое — под которым мы конкретно понимаем «ненаблюдаемое» прошлое, т. е. время перед тем, как мы, или кто-нибудь, или что-нибудь проводит данное наблюдение, — остаётся в обычном царстве квантовой неопределённости, в царстве вероятностей. Даже если мы прямо здесь и прямо сейчас зафиксировали положение электрона, то моментом раньше всё, что он имел, — это вероятность быть здесь, или там, или вообще где-то далеко.
Как мы видели, это не значит, что электрон (или любая частица) на самом деле находился только в одном из этих возможных положений, но мы просто не знаем, в каком. {87} Скорее, есть основания полагать, что электрон был во всех положениях, поскольку каждая из вероятностей — каждая из возможных историй — вносит вклад в то, что мы наблюдаем в настоящий момент. Вспомним, это доказывалось экспериментом, описанном в главе 4, в котором электроны пролетали через две щели. Классическая физика, которая опирается на широко разделяемое убеждение, что события имеют однозначные истории, говорит, что каждый электрон, попавший на экран детектора, прошёл либо через левую щель, либо через правую щель. Но такое представление о прошлом вводит в заблуждение: оно предсказывает результаты, показанные на рис. 4.3 а, которые не согласуются с тем, что происходит на самом деле (что показано на рис. 4.3 б). Наблюдаемая интерференционная картина может быть объяснена только чем-то, проходящим через обещели.
Квантовая физика обеспечивает именно такое объяснение, но при этом радикально меняет наши взгляды на прошлое — наше описание того, как отдельные события, которые мы наблюдаем, стали такими, какие есть. В соответствии с квантовой механикой вероятностная волна каждого электрона проходит через обещели, и, поскольку части волны, выходящие из каждой щели, смешиваются, итоговое распределение вероятности и, следовательно, места попадания электронов на экран демонстрируют интерференционную картину.
По сравнению с повседневным опытом, описание прошлого электрона в терминах накладывающихся волн вероятности совершенно необычно. Но, отбросив осторожность, вы можете предложить продвинуть это квантово-механическое описание ещё на один шаг дальше, что приведёт к ещё более причудливой возможности. Может быть, каждый отдельный электрон сам по себе на пути к экрану действительно проходит через обе щели, и итоговая картина является результатом интерференции этих двух классов историй. То есть имеется соблазн думать о волнах, выходящих из двух щелей, как о представляющих две возможные истории для индивидуального электрона — проходящего через левую щель или проходящего через правую щель, — и поскольку обе волны вносят вклад в то, что мы наблюдаем на экране, возможно, квантовая механика говорит нам, что обе потенциальные истории электрона вносят вклад в результат.
Удивительно, эта странная и чудесная идея — дитя разума нобелевского лауреата Ричарда Фейнмана, одного из самых оригинальных физиков XX в., — открывает весьма жизнеспособный путь размышлений о квантовой механике. Согласно Фейнману, если имеются альтернативные пути, по которым может быть достигнут заданный результат, — например, электрон попадает в некоторую точку на экране детектора, пролетев через левую щель, или попадает в ту же точку, но пролетев через правую щель, — тогда, в некотором смысле, все альтернативные варианты событий имеют место и происходят одновременно. Фейнман показал, что каждая такая история будет вносить вклад в вероятность того, что будет реализован их общий результат, и если эти вклады аккуратно сложить друг с другом, результат будет совпадать с полной вероятностью, которую предсказывает квантовая механика.
Фейнман назвал этот подход к квантовой механике суммированием по историям [42] ; этот подход показывает, что вероятностная волна объединяет все возможные варианты прошлого, которые могли предшествовать данному наблюдению, и хорошо иллюстрирует, что, для того чтобы достичь успеха там, где классическая физика терпит неудачу, квантовой механике приходится существенно расширять горизонты истории. {88}
В страну Оз
Существует другой вариант эксперимента с двойной щелью, в котором интерференция между альтернативными историями становится ещё более явной, поскольку два пути к экрану детектора разделены сильнее. Немного проще описывать эксперимент, используя фотоны вместо электронов, так что мы начинаем с источника фотонов — лазера — и выпускаем из него луч в направлении так называемого светоделителя. Этот прибор выполнен из полупрозрачного зеркала, типа такого, какие используются для скрытого наблюдения. Такое зеркало отражает половину падающего на него света, а другая половина проходит насквозь. Таким образом, исходный одиночный луч света расщепляется на два, левый и правый лучи, аналогично тому, что происходит с лучом света, который сталкивается с двумя щелями в двухщелевом опыте. Используя полностью отражающие зеркала, расположенные как показано на рис. 7.1, два луча снова собираются вместе и далее направляются к детектору. Рассматривая свет в виде волны, как в описании Максвелла, мы ожидаем увидеть — и, несомненно, видим — на экране интерференционную картину. Длина пути немного отличается для левого и правого маршрута, так что в то время как левый луч может достичь пика в заданной точке экрана детектора, правый луч может достичь пика, впадины или некоторого промежуточного состояния. Детектор записывает сумму интенсивностей двух волн, и поэтому мы получаем характерную интерференционную картину.
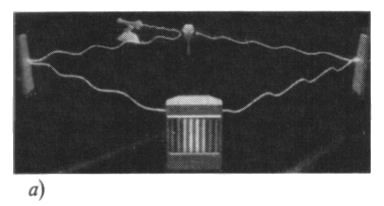

Рис. 7.1.( а) В эксперименте со светоделителем лазерный свет разделяется на два луча, которые идут двумя раздельными путями к экрану детектора. ( б) Интенсивность излучения лазера может быть снижена настолько, что он будет испускать отдельные фотоны; фотоны попадают на экран, со временем выстраивая интерференционную картину
Различие между классическим и квантовым станет очевидным, если мы значительно понизим интенсивность пучка лазера, так что он станет испускать одиночные фотоны, скажем, один в несколько секунд. Когда отдельный фотон попадает в светоделитель, классическая интуиция говорит, что он либо пройдёт насквозь, либо будет отражён. Классические рассуждения не допускают даже намёка на интерференцию, поскольку тут нечему интерферировать: всё, что мы имеем, это отдельные фотоны, проходящие от источника к детектору, один за другим, некоторые по левому пути, некоторые по правому. Но когда эксперимент завершён, то отдельные фотоны, регистрируемые всё это время (примерно как на рис. 4.4), даютинтерференционную картину, как на рис. 7.1 б. В соответствии с квантовой физикой причина этого состоит в том, что каждый зарегистрированный детектором фотон может дойти до детектора, двигаясь либо по левому пути, либо по правому. Так что мы обязаны объединить эти две возможные истории при определении вероятности того, что фотон попадёт на экран в ту или иную точку. Когда левая и правая вероятностные волны для каждого индивидуального фотона объединяются, они дают волнообразную вероятностную картину интерференции волн. Так что в отличие от Дороти, которая была сбита с толку, когда Страшила указал сразу налево и направо, показывая ей направление в страну Оз, результаты эксперимента с расщеплением пучка фотонов можно объяснить тем, что каждый фотон, направляясь к детектору, идёт сразу и левым, и правым путём.
42
В русскоязычной литературе чаще употребляется термин «суммирование по путям»или «интегрирование по путям»(или, в более общем случае, когда речь идёт не об отдельных частицах, а о квантованных полях, метод называется континуальным интегрированием). (Прим. ред.)
